Nape的几何相关笔记(GeomPoly)
Polygon 和 GeomPoly 的关系
Polygon 的构造函数和接收 GeomPoly.
Polygon 的 regular 算法
public static function regular(xRadius:Float, yRadius:Float, edgeCount:Int, angleOffset=0.0, weak:Bool=false):Array<Vec2> {
DEBUG(if(isNaN(xRadius) || isNaN(yRadius) || isNaN(angleOffset))
throw "Error: Polygon.regular cannot accept NaN arguments";
)
var ret = [];
var dangle = Math.PI*2/edgeCount;
for(i in 0...edgeCount) {
var ang = i*dangle + angleOffset;
var x = Vec2.get(Math.cos(ang)*xRadius,Math.sin(ang)*yRadius,weak);
ret.push(x);
}
return ret;
}多边形的分类
**三角形(**Triangular**)**是由三条线段顺次首尾相连,组成的一个闭合的平面图形是最基本的多边形
**凸多边形(****Convex)**的是一个内部为凸集的简单多边形.简单多边形的下列性质与其凸性等价:
- 每个内角小于或等于 180 度.
- 任何两个顶点间的线段位于多边形的内部或边界上. **Y 单调多边形(****Y-Monotone)** 任意水平线和这个多边形的交点至多只有两点的多边形

(图片来源:Monotone polygon)
上图中前两个都是单调多边形.
**凹多边形(****Concave)**:只要有一个内角大于 180 度,这个多边形就是凹的.
凹凸多边形的交互动画:
**简单多边形:**是指不相邻的边没有公共交点的多边形(The number of edges always equals the number of vertices)
Weakly-Simple 弱简单多边形
这个还不是很理解,多边形中间有空洞,通过给封闭区域加切线的方式转换过来应该就是弱简单多边形,具体可以参照下面两篇文章
3:Polygon(有中文)
多边形的关系
(图片来自nape_manual)

多边形的分解
为什么要有多边形分解的概念,因为 Shape 里面的
Polygon 只接受凸多边形(?).
simpleDecomposition 将一个复杂多边形转换成弱简单多边形(分解算法)
其他分解:
monotoneDecomposition, convexDecomposition 和 triangularDecomposition 将弱简单多边形转换成指定类型的多边形.(图片来自nape_manual)

多边形的简单化 (Simplification)
如果有几个点的距离很进,那一通过这个方法将这几个点合并成两个点,这就是简单化的基本思想.(图片来自nape_manual)
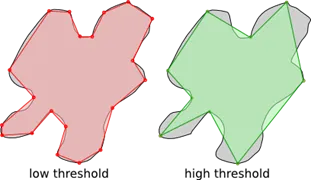 简单化相关讨论:
简单化相关讨论:
Re: Any way to speed-up or cache object creation?
理解 MarchingSquares 算法
利用 MarchingSquares 算法可以将一个不规则形状的轮廓通过一系列点来描述出来,
在不理解 MarchingSquares 算法的前提下看 Nape 里面 MarchingSquares 的 API 真是云里雾里,在参考了维基和 Nape 的具体表现后对这个算法有了一定的了解.
下面通过一个简单实例说明下其实现原理,这个实例用了一个简单的三角形做例子,对于复杂不规则多边形,思路是一样的.下图灰色的就是这个三角形,宽 400px,高 300px.
1.首先 MarchingSquares 需要将这个形状映射到一个网格上去,网格单元越小,精度越高,为了绘制方便我们假设网格尺寸是 100px(对于实际应用中,像素在 4-10 都是可以接受的),那么这个形状映射到网格就是这样的(黄线就是网格):
2:遍历所有网格顶点,并应用一个规则(isoFun)为所有顶点赋值.这里的 isoFun 按照特定应用需求可能不一样,最基本的类似于这样:如果顶点和这个形状接触返回-1,否则返回 1.
遍历之后如下图(图中红色表示不接触,绿色表示接触[-1])
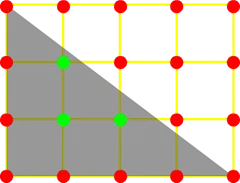
3:按照这样表(右下角)将每个小网格分割
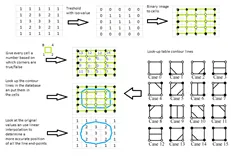 得到图形:
得到图形:
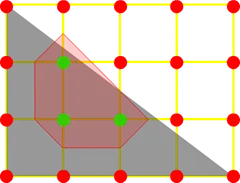
维基中最后一步还利用了一个叫”线性插值”的运算规则提高精度,但是在 Nape 中并没有找到这种方法.也就是说 Nape 在走到这里应该就停止并返回途中红色区域的所有点阵.
很明显这个精度明显是不够的,在 Nape 中通过一个叫 quality 的参数进行控制,上图就是 quality 是 0 的情况.
4:quality 参数的作用是对网格做进一步细分,下面演示当 quality 是 1 的情况.
可以将每个网格再分一次.如下图(灰线表示子网格轮廓)
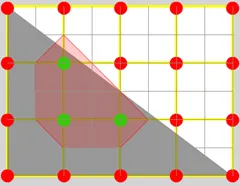
5:判断这些子网格顶点同样应用 isoFun 为次级顶点赋值得到的结果如下图(次级顶点小一点,从 trace 中能看出 nape 对遍历子网格做了优化并没有遍历全部而是只遍历红区域周围的):
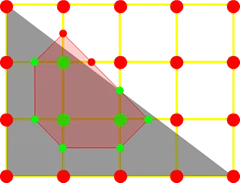
5.1:步骤 3 的连线规则是根据维基提供的一张表格来定义的,但是针对 5 这种情况没有一张现成的表可以参考,通过观察 Nape 得到的结果可以发现 3 中对应的那张表格其实可以更加一般化.我从 3 中拿两个出来进行说明:
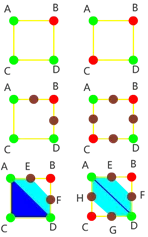
上图分别列举两种情况的分解过程(左边一组,右边一组).
其中第二行分别取他们红绿线的中点,然后用棕色原点表示.
对于第三行的结果这里分别用深蓝和浅蓝表示两种不同的区域,首先连接所有绿点确认深蓝区域,然后向棕色点延伸确认浅蓝色区域,得到的最终结果就是深蓝和浅蓝的合集区域(左:AEFDCA,右:AEFDGHA),为什么要分别用深蓝和浅蓝两种颜色区分呢,因为在确认和深蓝区域后浅蓝区域才好确认,否则第二列得到的结果可能就是 EBFDGHE 了.
同理将这个法则推广到更多点上来就比较容易了,拿 5 步骤配图中的第一块区域得到的结果就是:
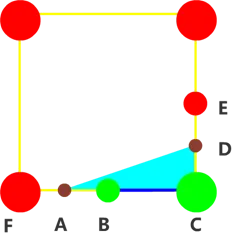
6:应用上述规则后最终得到的结果如下图:
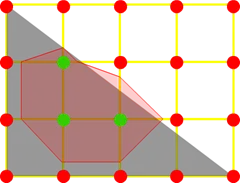
当这个 quality 很高时,结果是这样的:
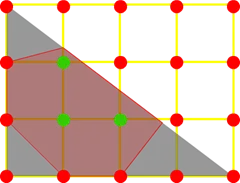
写到这里 Nape 里面的 MarchingSquares 算法实现就差不多了,在理解了算法之后看看 API 就很清楚了.
接受值
iso :: 一个实现了 nape.geom.IsoFunction 接口(iso)的类实例.(为何要用接口的形式可能和这篇文章指出的内存泄漏有关,但是我没有试出来..)
bounds :: 应用 MarchingSquares 算法的范围
cellsize :: 将 bounds 分成网格之后每个网格的大小,也就是上述例子里面的 100 像素.
quality :: 子网格的迭代次数,详见上述第 4 步之后说明.
subgrid :: 将 bounds 的大小再细分成 subgrid 定义个小范围,每个小范围继续使用 MarchingSquares 算法.subgrid 的大小要大于 cellsize 的大小,否则没有意义.
combine :: 如果是 true,将以 cellsize 大小为单位返回所有点阵,否则返回合并后的轮廓点
output :: 如果传入则返回值不是从 nape 资源池中取得 GeomPolyList,而是以 add 的形式加到这个传入的 GeomPolyList 里面.
返回值:一个 GeomPolyList,一般来说这个 list 的长度是 1,如果指定了 subgrid,那么这个长度就是 bounds 被 subgrid 分掉后的长度.
其他注意点
iso 的结果必须唯一,即给定 x 和 y 得到的值一定是同一个,符合数学里面函数的定义.这个函数可以是数学意义上的连续函数 比如圆的函数表达式
marching 算法返回的点阵不一定是凸多边形,所以需要进行多边形分解转换.参考:
New error after updating to latest build
其他 MarchingSquares 的讨论:
MarchingSquares 的维基参考资料: